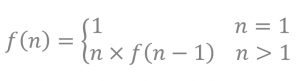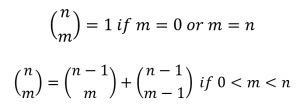آشنایی با توابع بازگشتی معروف و نحوه پیاده سازی آنها در پایتون
در این پست، ابتدا به معرفی روابط بازگشتی پرداخته می شود و سپس شما را با ۵ رابطه بازگشتی معروف اما در عین حال ساده آشنا می کنیم. در نهایت هر کدام از این الگوریتم ها را در زبان پایتون پیاده سازی می کنیم تا موضوع بیشتر جا بیافتد. پایتون به دلیل سادگی و سهولت در کدنویسی، برای درک مسائل الگوریتمی بسیار کاربردی است، به همین دلیل این زبان را برای پیاده سازی الگوریتم ها انتخاب نموده ایم.
رابطه بازگشتی چیست ؟
در ریاضیات به روابطی که به طور بازگشتی تعریف می شوند، روابط بازگشتی گفته می شود. هر رابطه بازگشتی دارای مرتبه خاصی است. به عنوان مثال مرتبه بازگشتی رابطه فاکتوریل n-1 است زیرا برای محاسبه جمله nام لازم است تا ابتدا n-1 جمله دیگر را محاسبه کنیم. یکی از چالش های مهم در ریاضیات، یافتن فرمول صریح برای روابط بازگشتی است. این کار از دو جهت حائز اهمیت می باشد: اول اینکه برای محاسبه جمله nام نیازی به محاسبه جملات قبلی نداریم. دوم اینکه زمان اجرای الگوریتم غالبا کاهش پیدا می کند. بر روی روابط بازگشتی دسته بندی های مختلفی انجام شده است از جمله: همگن، ناهمگن، خطی، غیر خطی و … در این مقاله به بررسی انواع روابط بازگشتی نمی پردازیم. می توانید برای اطلاعات بیشتر از منابع موجود در بستر اینترنت و کتاب های مرجع استفاده نمایید.
۱- فاکتوریل
تابع فاکتوریل در ریاضیات به صورت زیر تعریف می شود:
فاکتوریل هر عدد طبیعی در ریاضیات از حاصلضرب آن عدد در تمام اعداد صحیح و مثبت (اعداد طبیعی) کوچکتر از آن به دست میآید. فاکتوریل عددی مانند n را !n مینویسند و «اِن فاکتوریل» میخوانند. همچنین طبق قرارداد، فاکتوریل صفر همیشه برابر با یک است. برای کسب اطلاعات بیشتر در مورد فاکتوریل به این صفحه در ویکی پدیا مراجعه کنید.
الگوریتم بازگشتی: الگوریتم بازگشتی فاکتوریل، از یک رابطه ساده بدست می آید و آن این است که فاکتوریل عدد n برابر حاصل ضرب n در فاکتوریل عدد n-1 است. به عبارت دیگر برای محاسبه فاکتوریل یک عدد می توان آن عدد را در فاکتوریل عدد قبلی اش ضرب کرد. بر همین اساس قطعه کد زیر را در پایتون می نویسیم:
def fact(n):
if n==0:
return 1
else:
return n * fact(n-1)
۲- مجموع اعداد
برای محاسبه مجموع اعداد از ۱ تا n، باید اعداد ۱ تا n را با یکدیگر جمع کنیم.
الگوریتم بازگشتی: مجموع اعداد برای n عدد برابر است با n به علاوه ی مجموع اعداد برای n-1 عدد. همچنین مجموع عدد ۱ برابر ۱ می باشد. براساس این الگوریتم بازگشتی کد به صورت زیر نوشته می شود:
def my_sum(n):
if(n==1):
return 1
else:
return n + my_sum(n-1)
print my_sum(1)
۳- تابع توان
همانطور که می دانید، توان رساند یک عدد در واقع عبارت است از تعداد معینی ضرب. به عنوان مثال برای به توان رساندن عدد ۲ به توان ۳؛ کافی است عدد ۲ را ۳ بار در خودش ضرب کنیم.
الگوریتم بازگشتی: برای محاسبه n به توان m کافی است n را m بار در خودش ضرب کنیم. در نتیجه n به توان m برابر است با حاصل ضرب n، در n به توان m-1. کد مربوط به این الگوریتم را در زیر مشاهده می کنید:
def my_pow(n, m):
if(m==1):
return n
elif(m==0):
return 1
else:
return n * my_pow(n, m-1)
print my_pow(2, 0)
۴- تابع ترکیب
به هر انتخاب غیر مرتب r شی از n شی داده شده یک ترکیب r شی ازاین n شی گفته میشود. (ویکی پدیا)
الگوریتم بازگشتی: برای پیاده سازی این تابع به صورت بازگشتی، از این فرمول استفاده می کنیم: اگر r برابر ۰ باشد و یا r برابر n باشد جواب ترکیب برابر ۱ است.
def combination(m, n):
if m==0 or m==n:
return 1
else:
return combination(m, n-1) + combination(m-1, n-1)
۵- تابع تقسیم صحیح بر صحیح
این نوع تقسیم، نوعی از تقصیم دو عدد صحیح بر هم است. برای اطلاعات بیشتر می توانید در این باره جستجو کنید. در تصویر زیر تابع ریاضی تقسیم صحیح بر صحیح را مشاهده می کنید:
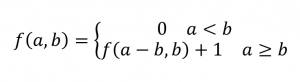 الگوریتم بازگشتی: اگر مقسوم علیه از مقسوم بزرگتر باشد خروجی تابع برابر ۰ است. در غیر اینصورت مقسوم علیه را از مقسوم کم کرده و دوباره عملیات تقسیم را ادامه می دهیم. این کار تا زمانی انجام می شود که مقسوم بزرگتر یا مساوی مقسوم علیه باشد. کد زیر این تابع را در زبان پایتون نمایش می دهد:
الگوریتم بازگشتی: اگر مقسوم علیه از مقسوم بزرگتر باشد خروجی تابع برابر ۰ است. در غیر اینصورت مقسوم علیه را از مقسوم کم کرده و دوباره عملیات تقسیم را ادامه می دهیم. این کار تا زمانی انجام می شود که مقسوم بزرگتر یا مساوی مقسوم علیه باشد. کد زیر این تابع را در زبان پایتون نمایش می دهد:
def div(a, b):
if b==0:
return
if a<b:
return 0
else:
return div(a-b, b) + 1
نتیجه گیری
در این پست تنها به معرفی چند تابع بازگشتی معروف پرداخته شد. اما جدا از بحث پیاده سازی یک الگوریتم، مرتبه زمانی آن نقش مهمی را ایفا می کند. این که یک الگوریتم در تعداد اجراهای زیاد در چه زمانی می تواند خروجی مناسب را تولید کند بحثی است که در این مقاله بدان پرداخته نشد. برای اطلاع از این موارد می توانید در رابطه با O Notation تحقیق کنید. اگر سوال یا انتقادی داشتید می توانید در بخش نظرات با من در میان بگذارید.